Spherical Trigonometry
Spherical Triangles are triangles projected onto the surface of a sphere.
They are useful in astronomical calculations, crystallography, and other efforts
involving the analysis of objects rotating around a fixed point.
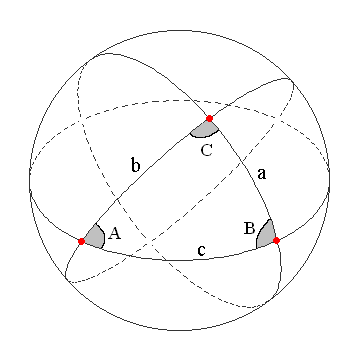 Consider the triangle formed by 3 points on the surface of a sphere: A, B, and C.
By convention, we label the sides opposite the points with the lower case letter
corresponding to the vertex opposite the side.
So the side we might want to call "BC" actually gets labelled "a".
Let "O" be the origin, or the center of the sphere.
The length of the side "a" is given by the angle BOC.
Similarly the side "b" has length AOC and side "c" has length AOB.
The angle at the vertex A is the dihedral angle between the planes
AOB and AOC. Given these definitions, we have completely described
a spherical triangle and can now discuss the handful of important theorems
that make their analysis useful:
Consider the triangle formed by 3 points on the surface of a sphere: A, B, and C.
By convention, we label the sides opposite the points with the lower case letter
corresponding to the vertex opposite the side.
So the side we might want to call "BC" actually gets labelled "a".
Let "O" be the origin, or the center of the sphere.
The length of the side "a" is given by the angle BOC.
Similarly the side "b" has length AOC and side "c" has length AOB.
The angle at the vertex A is the dihedral angle between the planes
AOB and AOC. Given these definitions, we have completely described
a spherical triangle and can now discuss the handful of important theorems
that make their analysis useful:
The cosine rule
cos(a) = cos(b) * cos(c) + sin(b) * sin(c) * cos(A)
The transposed cosine rule
sin(a) * cos(B) = cos(b) * sin(c) - sin(b) * cos(c) * cos(A)
The sine rule
sin(a) / sin(A) = sin(b) / sin(B) = sin(c) / sin(C)
The four parts rule (usually written with cotangents)
cos(a) * cos(C) = sin(a) * cos(b)/sin(b) - sin(C) * cos(B)/sin(B)
The cosine rule for the angles
(also known as the polar cosine rule
cos(A) = -cos(B) * cos(C) + sin(B) * sin(C) * cos(a)
The polar transposed cosine rule:
sin(A) * cos(b) = cos(B) * sin(C) + sin(B) * cos(C) * cos(a)
Trigonometric Identities
These should be old friends from high school for most people:
tan(x) = sin(x) / cos(x)
sin(x)*sin(x) + cos(x)*cos(x) = 1
cos(90-x) = sin(x)
sin(90-x) = cos(x)
sin(90+x) = cos(x)
cos(90+x) = -sin(x)
sin(-x) = -sin(x)
cos(-x) = cos(x)
sin(180-x) = sin(x)
cos(180-x) = -cos(x)
sin(x+180) = -sin(x)
cos(x+180) = -cos(x)
Have any comments? Questions?
Drop me a line!
Tom's home page / tom@mmto.org
 Consider the triangle formed by 3 points on the surface of a sphere: A, B, and C.
By convention, we label the sides opposite the points with the lower case letter
corresponding to the vertex opposite the side.
So the side we might want to call "BC" actually gets labelled "a".
Let "O" be the origin, or the center of the sphere.
The length of the side "a" is given by the angle BOC.
Similarly the side "b" has length AOC and side "c" has length AOB.
The angle at the vertex A is the dihedral angle between the planes
AOB and AOC. Given these definitions, we have completely described
a spherical triangle and can now discuss the handful of important theorems
that make their analysis useful:
Consider the triangle formed by 3 points on the surface of a sphere: A, B, and C.
By convention, we label the sides opposite the points with the lower case letter
corresponding to the vertex opposite the side.
So the side we might want to call "BC" actually gets labelled "a".
Let "O" be the origin, or the center of the sphere.
The length of the side "a" is given by the angle BOC.
Similarly the side "b" has length AOC and side "c" has length AOB.
The angle at the vertex A is the dihedral angle between the planes
AOB and AOC. Given these definitions, we have completely described
a spherical triangle and can now discuss the handful of important theorems
that make their analysis useful: